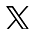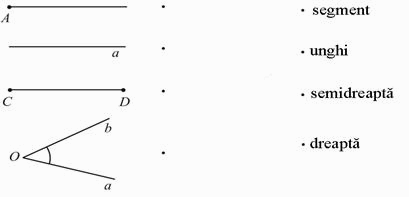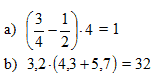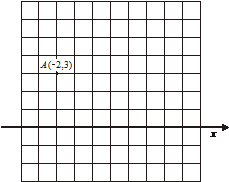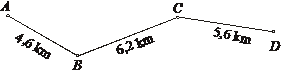PRAVILNIK O PROGRAMU ZAVRŠNOG ISPITA U OSNOVNOM OBRAZOVANJU I VASPITANJU("Sl. glasnik RS - Prosvetni glasnik", br. 1/2011, 1/2012, 1/2014, 12/2014, 2/2018, 3/2021, 14/2022, 4/2023 i 5/2023 - ispr.) |
3. GRAMATICA, LEXICUL, LIMBA ROMÂNĂ LITERARĂ
În domeniul GRAMATICA elevul/eleva trebuie:
LR.3.3.1. să aplice regulile de despărţire a cuvintelor în silabe
|
Exerciţiu |
|
Completaţi următoarea regulă privitoare la despărţirea cuvintelor în silabe, încercuind una din variantele date sub a, b sau c: a) cuvântul jertfă se
desparte: jert-fă, pentru că pronunţarea grupului tf în aceeaşi
silabă nu este posibilă. |
|
Răspuns |
|
a) |
LR.3.3.2. să cunoască noţiunile de fonetică a limbii române
|
Exerciţiu |
|
Citiţi cu atenţie următoarele cuvinte: Scrieţi care din aceste cuvinte au în
componenţa lor: |
|
Răspuns |
|
Triftongi: leoaică, beai |
LR.3.3.3. să analizeze părţile de vorbire ţinând cont de categoriile gramaticale
|
Exerciţiu |
|
Analizaţi cuvintele subliniate prin intermediul tuturor categoriilor gramaticale pe care le au: Dar fiindcă mi-au ieşit până acum înainte încă doi spâni şi cu tine al treilea, apoi mai îmi vine a crede că aceasta-i ţara spânilor şi n-am încotro. |
|
Răspuns |
|
au ieşit - verb predicativ, modul indicativ,
timpul perfect compus, persoana a treia, plural |
LR.3.3.5. să scrie felurile propoziţiilor coordonate şi subordonate în frază şi ortografia lor
|
Exerciţiu |
|
Determinaţi felul propoziţiilor subliniate: Am făcut o greşeală care nu se mai
repară. |
|
Răspuns |
|
- propoziţie subordonată atributivă - propoziţie completivă directă - propoziţie circumstanţială de mod |
LR.3.3.6. să ştie să găsească sensul unui cuvânt necunoscut şi să-l aplice în vorbirea cotidiană
|
Exerciţiu |
|
Se dă textul: "Să râzi, nu de greşelile pe care nu le faci, ci de acelea pe care nu le-ai făcut niciodată, deşi ai fi avut prilej să le faci." I. Citiţi textul cu atenţie şi găsiţi sinonime şi omonime pentru trei cuvinte din text; _________________________________________________________________ |
|
Răspuns |
|
Sinonime: a râde - a se bucura,
greşeală - eroare, niciodată - nicicând |
În domeniul LEXICUL elevul/eleva trebuie:
LR.3.3.7. să folosească cuvintele şi expresiile însuşite în toate situaţiile de comunicare
|
Exerciţiu |
|
Alegeţi antonimul cuvântului subliniat din propoziţia: "Glasul său ascuţit străbate valea." a) strident |
|
Răspuns |
|
c) |
LR.3.3.8. să recunoască termenii lexicali utilizaţi în diferite texte literare şi neliterare
|
Exerciţiu |
|
A fost odată ca niciodată (…) (Greuceanu) I. Identificaţi în text un cuvânt omonim şi
precizaţi sensurile lui. ___________________________________________________________________ |
|
Răspuns |
|
|
LR.3.3.9. să distingă formele de exprimare literară şi dialectală
|
Exerciţiu |
|
Transcrieţi propoziţiile în limba română standard: Iei or fost la scăldat în Dunăre. |
|
Răspuns |
|
Ei au fost să facă baie în Dunăre. |
În domeniul LIMBA ROMÂNĂ LITERARĂ elevul/eleva trebuie:
LR.3.3.10. să cultive varianta literară a limbii române în toate situaţiile de comunicare
|
Exerciţiu |
||||||||
|
Completaţi spaţiile punctate cu forma corectă a cuvintelor:
|
||||||||
|
Răspuns |
||||||||
|
În domeniul LITERATURA elevul/eleva trebuie:
LR.3.4.1. să recunoască titlul operei literare, autorul, genul şi speciile literare pe baza fragmentelor date, personajelor caracteristice, temelor şi motivelor
|
Exerciţiu |
|
În baza numelui autorului şi personajelor
care sunt date în paranteză scrieţi pe linie titlul operei literare: |
|
Răspuns |
|
. O scrisoare pierdută Amintiri din copilărie |
LR.3.4.2. să recunoască caracteristicile esenţiale ale genurilor literare într-un anumit text
|
Exerciţiu |
|
Urmăriţi cu atenţie fragmentul din Ploaie la Nada Florilor de Mihail Sadoveanu: "Soarele a pălit cam tare, îmi zise Culai, peştele a fost destul de spuzit de sare, aşa încât îmi închipui că ţi-i este..... Îmi era sete, se uscase limba în gură; însă îmi făceam socoteala că trebuie să mai rabd. Apa din jurul ostrovului era plină de gângănii mari şi mărunte, pe care le vedeam cu ochii; şi de altele şi mai mărunte pentru care, ca să le deosebesc, aş fi avut nevoie de instrumentele din laboratorul gimnaziului nostru." Răspundeţi pe liniile alăturate: A. Cărui gen literar aparţine opera: B. Modul de expunere prin care scriitorul ne
dezvăluie ideile şi sentimentele sale cu ajutorul acţiunii şi personajelor se
numeşte |
|
Răspuns |
|
A) genul epic B) naraţiune |
LR.3.4.3. să determine figurile de stil în operele literare
|
Exerciţiu |
|
Citeşte fragmentul de mai jos: "Conul Vasile e scund şi slab; are nasul ascuţit, iar umerii obrajilor îi lasă, în urmă de tot, ochii adânciţi în fundul capului, înconjuraţi de cearcăne întunecate." Cu ajutorul cărei figuri de stil este
realizată descrierea acestui personaj? |
|
Răspuns |
|
epitet |
LR.3.4.4. să analizeze operele literare citite
|
Exerciţiu |
|
Stau câteodată şi-mi aduc aminte ce vremi şi ce oameni mai erau în părţile noastre pe când începusem şi eu, drăgăliţă-Doamne, a mă ridica băieţaş la casa părinţilor mei, în satul Humuleşti, din târg drept peste apa Neamţului; sat mare şi vesel, împărţit în trei părţi, care se ţin tot de una: Vatra satului, Delenii şi Bejenii. Ş-apoi Humuleştii, şi pe vremea aceea, nu erau numai aşa, un sat de oameni fără căpătâi, ci sat vechi răzăşesc, întemeiat în toată puterea cuvântului: cu gospodari tot unul şi unul, cu flăcăi voinici şi fete mândre, care ştiau a învârti şi hora, dar şi suveica, de vuia satul de vatale în toate părţile; cu biserică frumoasă şi nişte preoţi şi dascăli şi poporeni ca aceia, de făceau mare cinste satului lor. Şi părintele Ioan de sub deal, Doamne, ce om vrednic şi cu bunătate mai era! Prin îndemnul său, ce mai pomi s-au pus în ţintirim, care era îngrădit cu zăplaz de bârne, streşinit cu şindilă, şi ce chilie durată s-a făcut la poarta bisericii pentru şcoală; ş-apoi, să fi văzut pe neobositul părinte cum umbla prin sat din casă în casă, împreună cu bădiţa Vasile a Ilioaei, dascălul bisericii, un holtei zdravăn, frumos şi voinic, şi sfătuia pe oameni să-şi dea copiii la învăţătură. Şi unde nu s-au adunat o mulţime de băieţi şi fete la şcoală, între care eram şi eu, un băiat prizărit, ruşinos şi fricos şi de umbra mea. Şi cea dintâi şcolăriţă a fost însăşi Smărăndiţa popii, o zgâtie de copilă ageră la minte şi aşa de silitoare, de întrecea mai pe toţi băieţii şi din carte, dar şi din nebunii. Însă părintele mai în toată ziua da pe la şcoală şi vedea ce se petrece... Şi ne pomenim într-una din zile că părintele vine la şcoală şi ne aduce un scaun nou şi lung, şi după ce-a întrebat de dascăl, care cum ne purtăm, a stat puţin pe gânduri, apoi a pus nume scaunului Calul Balan şi l-a lăsat în şcoală. În altă zi ne trezim că iar vine părintele la şcoală, cu moş Fotea, cojocarul satului, care ne aduce, dar de şcoală nouă, un drăguţ de biciuşor de curele, împletit frumos, şi părintele îi pune nume Sfântul Nicolai, după cum este şi hramul bisericii din Humuleşti... Apoi pofteşte pe moş Fotea că, dacă i-or mai pica ceva curele bune, să mai facă aşa, din când în când, câte unul, şi ceva mai grosuţ, dacă se poate... Bădiţa Vasile a zâmbit atunci, iară noi, şcolarii, am rămas cu ochii holbaţi unii la alţii. Şi a pus părintele pravilă şi a zis că în toată sâmbăta să se procitească băieţii şi fetele, adică să asculte dascălul pe fiecare de tot ce-a învăţat peste săptămână; şi câte greşeli va face să i le însemne cu cărbune pe ceva, iar la urma urmelor, de fiecare greşeală să-i ardă şcolarului câte un sfânt-Nicolai. Atunci copila părintelui, cum era sprinţară şi plină de incuri, a bufnit în râs. Păcatul ei, sărmana! - Ia, poftim de încalecă pe Balan, jupâneasă! zise părintele, de tot posomorât, să facem pocinog sfântului Nicolai cel din cui. Şi cu toată stăruinţa lui Moş Fotea şi a lui bădiţa Vasile, Smărăndiţa a mâncat papara…Noi, când am văzut asta, am rămas înlemniţi. Iar părintele, ba azi, ba mâine, aducând pitaci şi colaci din biserică, a împărţit la fiecare, de ne-a îmblânzit, şi treaba mergea strună; băieţii schimbau tabla în toate zilele, şi sâmbăta procitanie. Nu-i vorbă, că noi tot ne făceam felul, aşa, câteodată; căci, din băţul în care era aşezată fila cu cruce-ajută şi buchile scrise de bădiţa Vasile pentru fiecare, am ajuns la trătaji, de la trătaji la ceaslov, ş-apoi, dă, Doamne, bine! în lipsa părintelui şi a dascălului intram în ţinterim, ţineam ceaslovul deschis, şi, cum erau filele cam unse, trăgeau muştele şi bondarii la ele, şi, când clămpăneam ceaslovul, câte zece-douăzeci de suflete prăpădeam deodată; potop era pe capul muştelor! Într-una din zile, ce-i vine părintelui, ne caută ceasloaveleşi, când le vede aşa sângerate cum erau, îşi pune mâinile în cap de necaz. Răspundeţi la următoarele întrebări: 1. Scrieţi titlul operei literare din care este fragmentul dat. 2. Spuneţi dacă în acest fragment avem momente autobiografice ale autorului. 3. Subliniaţi propoziţiile unde se dau trăsăturile fizice şi morale ale autorului şi ale Smărăndiţei. |
|
Răspuns |
|
1. Amintiri din copilărie 2. Da, avem 3. Şi unde nu s-au adunat o mulţime de băieţi şi fete la şcoală, între care eram şi eu, un băiat prizărit, ruşinos şi fricos şi de umbra mea. Şi cea dintâi şcolăriţă a fost însăşi Smărăndiţa popii, o zgâtie de copilă ageră la minte şi aşa de silitoare, de întrecea mai pe toţi băieţii şi din carte, dar şi din nebunii. |
LR.3.4.6. să prezinte atitudinea personală despre textele citite şi să o prezinte argumentat
|
Exerciţiu |
|
Citeşte cu atenţie colindul următor: "În vârfuţul muntelui, (Mioriţa, colind din Transilvania) Scrie o compunere în care să argumentezi
faptul că creaţia Mioriţa este un colind şi nu o baladă populară. |
|
Răspuns |
|
|
LR.3.4.7. să respecte metodologia lucrărilor scrise
|
Exerciţiu |
|
Aranjaţi enunţurile de mai jos astfel încât să alcătuiască un text. Am scos din pachet un sandviş şi i l-am dat.
* Mergeam spre şcoală. * Avea o Blăniţă tărcată şi mustăţile mari i se mişcau
încet. * Am înţeles imediat că familia noastră o să se mărească în curând. *
Am vrut să îmi continuu drumul, dar am constatat că mă urmează cuminte. * |
|
Răspuns |
|
Mergeam spre şcoală. Deodată, mi-a apărut în faţă o pisică. Avea o blăniţă tărcată şi mustăţile mari i se mişcau încet. Am scos din pachet un sandviş şi i l-am dat. Am vrut să îmi continuu drumul, dar am constatat că mă urmează. Mă privea galeş şi torcea încet. Privirile noastre s-au întâlnit uimite. Am înţeles imediat că familia noastră o să se mărească în curănd. |
Standarde de învăţământ pentru finalizarea învăţământului obligatoriu la limba română care vor fi examinate cu exerciţii necunoscute
LR.2.1.4. face diferenţa dintre toate părţile textului şi ale cărţii, inclusiv indicele de nume, literatura de specialitate şi dicţionarul de terminologie literară
|
Exerciţiu |
|
În faţa ta se află o pagină a indicelui de cuvinte din Dicţionarul frazeologic al limbii române. Priveşte cu atenţie şi răspunde la întrebarea pusă.
Ce înseamnă numărul de după noţiunea din
indice? a) numărul paragrafului în care se
vorbeşte despre acea noţiune |
|
Răspuns |
|
b) |
LR.2.1.6. face distincţia dintre subiectivitatea şi obiectivitatea informaţiilor dintr-un text citit
|
Exerciţiu |
|
Citiţi cu atenţie textul de mai jos şi subliniaţi fragmentul în care informaţiile sunt redate într-un mod argumentat: "Soarele scapătă spre asfinţit.
Crestele munţilor par aprinse. Încet, se desfac şi s-aştern pe văi perdele de
umbră. |
|
Răspuns |
|
Frumuseţea şi caracterul maiestuos al Dunării au constituit frecvent surse de inspiraţie pentru poeţi, pictori, muzicieni şi alţi oameni de cultură? Cea mai cunoscută creaţie culturală dedicată fluvului este "Dunărea albastră", un vals vienez creat de Johan Strauss Tânărul în 1886 care a devenit un imn neoficial al Vienei Imperiale. |
LR.3.1.4. face paralelă între informaţiile din mai multe texte de structură mai complexă
|
Exerciţiu |
|
Citeşte cu atenţie două texte scrise de autori diferiţi despre comportamentul violent al tinerilor. Compară atitudinile lor referitoare la violenţă. Autorul 1: Recent au fost organizate în 40 de şcoli
cercetări referitoare la violenţa în rândurile elevilor. S-a constatat că în
relaţia victimă-agresor nu participă 58% din elevi. Cu alte cuvinte, doar 58%
nu sunt nici victime, nici agresori. Înseamnă că ceva mai puţin de jumătate
din numărul total al elevilor, mai exact 42%, apar în "cercul
violenţei", fie ca victime, fie ca agresori. În rolul de victime ale
violenţelor numărul elevilor este prea mare, chiar 37%. Autorul 2: Cel mai mare număr de elevi au declarat că
în timpul şcolarizării lor, în timpul cursurilor sau după ore, au fost supuşi
luării în derâdere, jignirilor, li s-au dat porecle prin care erau
dispreţuiţi. Ei amintesc de asemenea şi alte neplăceri: luarea necuviincioasă
peste picior, răspândirea minciunilor despre ei, convingerea altor elevi să
nu fie prieteni cu ei. Încercuieşte litera din faţa afirmaţiei exacte. a) ambii autori doar au expus date, fără
atitudine în legătură cu problema cercetată |
|
Răspuns |
|
c) |
LR.3.3.4. să facă distincţia dintre unităţile sintactice în propoziţie şi frază
|
Exerciţiu |
|
1. Analizaţi cuvântul subliniat din
următoarele versuri: ţinând cont de: Acest cuvânt ca parte de propoziţie este un______________________ şi el determină un verb ____________________ |
|
Răspuns |
|
a) am semănat Acest cuvânt ca parte de propoziţie este un complement direct şi el determină un verb tranzitiv. |
LR.3.4.5. să analizeze trăsăturile fizice şi morale ale personajelor din text
|
Exerciţiu |
|
Citeşte fragmentul dat şi răspunde la
următoarele cerinţe: 1) Fata amintită este personajul literar ______________________ din nuvela _____________________ de scriitorul ____________________. 2) Extrage din fragment cuvintele
prin care ni se redă înfâţişarea fizică şi morală a personajului.
|
|
Răspuns |
|
1) Sanda; Scormon; Ioan Slavici |
Normele nivelului de cunoştinţe pentru matematică, cu exemple de probleme, care se plică la sfârşitul ciclului de învăţământ obligatoriu
МА.1.1.1. Elevul trebuie să ştie să citească şi să scrie diferite feluri de numere (naturale, întregi, raţionale).
|
Problema |
|
Leagă prin linii numerele egale, aşa cum prezintă imaginea:
|
|
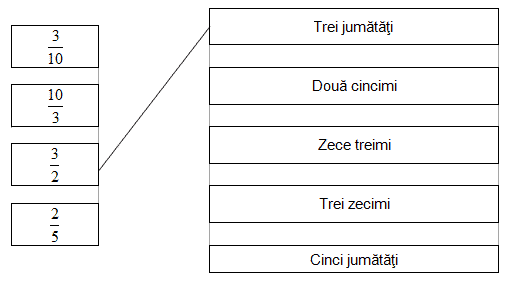
Soluţia |
|
|
МА.1.1.2. Elevul trebuie să ştie să transcrie numărul din forma zecimală în formă de fracţie.
|
Problema |
|
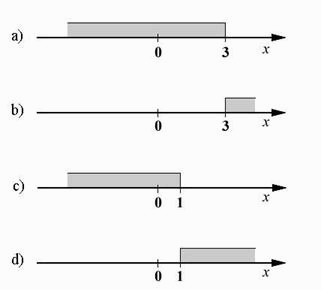
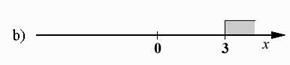
Care dintre numerele date este egal cu numărul 0,3? Înconjoară litera din faţa răspunsului corect. a) b) c) d)
|
|
Soluţia |
|
b) |
МА.1.1.3. Elevul trebuie să ştie să compare, după mărime, numerele scrise în aceeaşi formă, cu ajutorul reprezentărilor grafice necesare.
|
Problema |
||||||||||||||||||
|
Fie numerele:
|
||||||||||||||||||
|
Soluţia |
||||||||||||||||||
|
|
||||||||||||||||||
МА.1.1.4. Elevul trebuie să ştie să efectueze o operaţie elementară de calcul cu numere scrise în aceeaşi formă, folosind reprezentările grafice, atunci când este necesar (adunarea şi scăderea fracţiilor numai dacă au acelaşi numitor); să calculeze, de exemplu: 1/5 din n, dacă n este un număr natural dat.
|
Problema |
|
Calculează şi scrie rezultatul corespunzător: a) - 6 : 2 = ________ b) - 6 - 2 = ________ c) - 6 ∙ 2 = ________ d) - 6 + 2 = ________
|
|
Soluţia |
|
a) - 6 : 2 = -3 b) - 6 - 2 = -8 c) - 6 ∙ 2 = -12 d) - 6 + 2 = -4 |
МА.1.1.5. Elevul trebuie să ştie să efectueze împărţirea cu rest printr-un număr de o cifră şi să ştie când este un număr divizibil cu alt număr.
|
Problema |
|||||||||||||||
|
Completează tabelul care urmează aşa cum este indicat:
|
|||||||||||||||
|
Soluţia |
|||||||||||||||
|
МА.1.1.6. Elevul trebuie să ştie să folosească numerele întregi şi expresii mai simple care conţin numere întregi, aplicând reprezentări vizuale.
|
Problema |
|
Astăzi este ziua de naştere a Ioanei şi ea
zice: "Peste trei ani, voi avea 18 ani." Înconjoară litera din faţa răspunsului corect. а) 12 b) 15 c) 18 d) 21 |
|
Soluţie |
|
b) 15 |
МА.1.2.1. Elevul trebuie să efectueze operaţii formale reduse care depind de interpretare; trebuie să ştie să rezolve ecuaţii liniare, în care necunoscuta apare numai într-un membru.
|
Problema |
|
Ce număr este soluţia ecuaţiei Înconjoară litera din faţa răspunsului corect. а) 5 b) 6 c) 12 d) 20 |
|
Soluţia |
|
c) 12 |
МА.1.2.2. Elevul trebuie să efectueze operaţii formale reduse care depind de interpretare; trebuie să ştie să calculeze puterea unui număr dat şi să ştie operaţiile de bază cu puteri.
|
Problema |
|
Înconjoară litera din faţa răspunsului
corect. а) 25 b) 28 c) 212 d) 220 |
|
Soluţia |
|
c) 212 |
|
Problema |
|
Înconjoară litera din faţa răspunsului
corect. а) 0,06 b) 0,6 c) 0,09 d) 0,9 |
|
Soluţia |
|
c) 0,09 |
МА.1.2.3. Elevul trebuie să efectueze operaţii formale reduse care depind de interpretare; să adune, să scadă şi să înmulţească monoame.
|
Problema |
|
Scrie mai simplu expresiile: 5a3 + 7a3 = ___________ 9x2 - 4x2 = ____________ 2b · 3b2 = ______________
|
|
Soluţia |
|
5a3 + 7a3 = 12a3 9x2 - 4x2 = 5x2 2b · 3b2 = 6b3 |
МА.1.2.4. Elevul trebuie să efectueze operaţii formale reduse care depind de interpretare; să determine valoarea funcţiei care este dată prin tabel sau formulă.
|
Problema |
||||||||
|
Funcţia este dată prin formula y = 2x + 1. Determină valorile corespunzătoare ale variabilelor x şi y şi completează tabelul.
|
||||||||
|
Soluţia |
||||||||
|
|
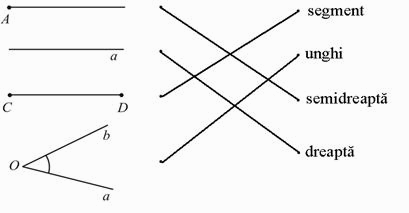
МА.1.3.1. Elevul trebuie să dispună de noţiunile: segment, semidreaptă, dreaptă, plan şi unghi (să recunoască modelele acestora în situaţii reale şi să ştie să le deseneze cu ajutorul instrumentelor; să facă diferenţa între unghiuri şi între dreptele paralele şi perpendiculare).
|
Problema |
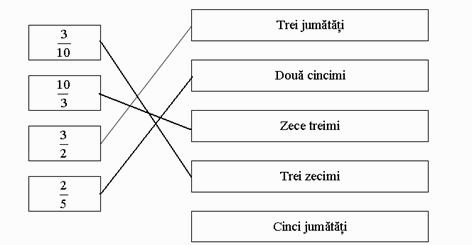
|
Leagă imaginea şi denumirea figurii pe care o reprezintă.
|
|
Soluţia |
|
|
МА.1.3.2. Elevul trebuie să dispună de noţiunile de: triunghi, patrulater, pătrat şi dreptunghi (să recunoască modelele acestora în situaţii reale şi să ştie să le deseneze cu ajutorul instrumentelor; elevul trebuie să facă diferenţa între diferite feluri de triunghiuri şi să ştie să calculeze perimetrul şi aria triunghiului, a pătratului şi a dreptunghiului cu ajutorul elementelor care figurează direct în problema dată; să ştie să calculeze latura necunoscută a triunghiului dreptunghic, aplicând teorema lui Pitagora).
|
Problema |
|
Care este aria suprafeţei de pardoseală pe care o acoperă un covor a cărui lungime are 3,5 m iar lăţimea are 2 m? Înconjoară litera din faţa răspunsului corect. а) 11 m2 b) 7 m2 c) 5,5 m2 d) 3,5 m2 |
|
Soluţia |
|
б) 7 m2 |
|
Problema |
|
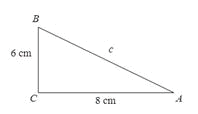
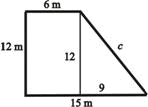
Calculează ipotenuza triunghiului dreptunghic desenat în imagine. c = _____cm |
|
Soluţia |
|
c = 10 cm |
МА.1.3.3. Elevul să dispună de noţiunea de cerc şi linie circulară (să distingă elementele lor de bază, să recunoască modelele acestora în situaţii reale şi să ştie să le deseneze cu ajutorul instrumentelor; să ştie să calculeze lungimea circumferinţei şi aria cercului de rază dată).
|
Problema |
|
Care este lungimea cercului a cărui rază are 7 cm? Înconjoară litera din faţa răspunsului corect. а) 14 cm b) 49 cm c) 14p cm d) 49p cm |
|
Soluţia |
|
c) 14p cm |
МА.1.3.4. Elevul să dispună de noţiunile de cub şi paralelipiped (să recunoască modelele acestora în situaţii reale, să ştie elementele de bază şi să ştie să calculeze ariile şi volumele acestora).
|
Problema |
|
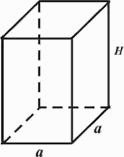
Muchia bazei unei prisme patrulatere
regulate are 6 cm, iar inălţimea prismei are Aria prismei este ___________ cm2. |
|
Soluţia |
|
A = 2 • 36 cm2 + 4 • 60 cm2 = 312 cm2 |
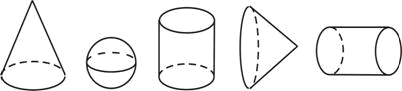
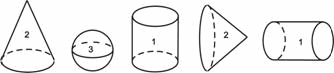
МА.1.3.5. Eevul trebuie să dispună de noţiunile de con, cilindru şi sferă (să recunoască modelele acestora în situaţii realesă şi ştie elementele lor de bază).
|
Problema |
|||
|
Scrie numărul 1, pe fiecare cilindru, numărul 2, pe fiecare con şi numărul 3, pe fiecare sferă.
|
|||
Soluţia |
|||
|
|
МА.1.3.6. Elevul să înţeleagă intuitiv noţiunea de figuri congruente (prin aducerea la suprapunere).
|
Problema |
||||||||||
|
||||||||||
| Soluţia |
||||||||||
|
c)
|
|
Problema |
|
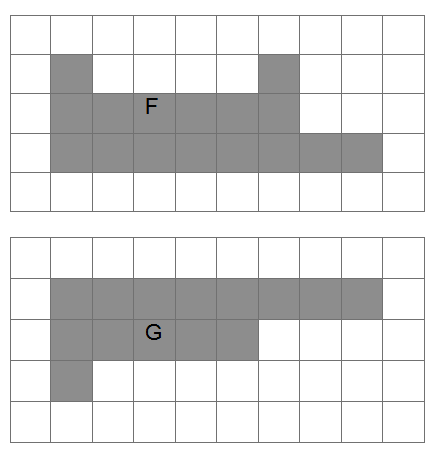
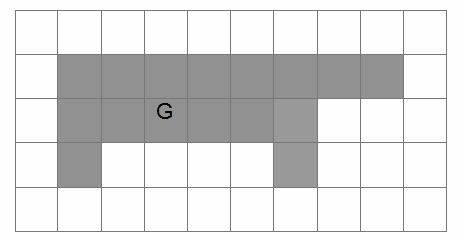
Fie figura F. Colorează ce mai este necesar pentru ca figura G să fie congruentă (să se poată suprapune) cu figura F.
|
|
Soluţia |
|
|
MA.1.4.1. Elevul trebuie să ştie să folosească măsurile adecuate cu care măsurăm lungimea, aria, volumul, masa, timpul şi unghiurile.
|
Problema |
|||||||||||||||
|
Completează spaţiul liber, din tabel, cu unitatea corespunzătoare.
|
|||||||||||||||
|
Soluţia |
|||||||||||||||
|
|
МА.1.4.2. Elevul trebuie să ştie să transforme unităţile pentru lungime, masă şi timp în unităţi mai mici.
|
Problema |
|
Care perioadă de timp este cea mai lungă? Înconjoară litera din faţa răspunsului corect. а) trei luni; b) 100 de zile; c) 10 săptămâni; d) un sfert din an. |
|
Soluţia |
|
b) 100 de zile. |
МА.1.4.3. Elevul trebuie să ştie să folosească apoene băneşti diferite.
|
Problema |
|
3 bancnote a câte 200 de dinari, le schimbi în bancnote a câte 50 de dinari. Câte bancnote vei avea?
Voi avea ______ bancnote a câte 50 de dinari. |
|
Soluţia |
|
Voi avea 12 bancnote a câte 50 de dinari. |
МА.1.4.4. Elevul ştie să aleagă unitatea de măsură corspunzătoare atunci când trebuie să efectueze o măsurare; să aproximeze mărimile exprimate printr-o măsură anume.
|
Problema |
||||||||||||||||||
|
În spaţiul liber, scrie unitatea de măsură corespunzătoare (km, cm, l, kg sau g).
|
||||||||||||||||||
|
Soluţia |
||||||||||||||||||
|
|
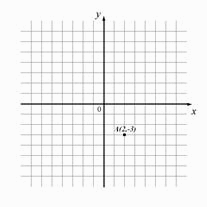
МА.1.5.1. Elevul trebuie să ştie să exprime poziţia obiectelor sortându-le pe linii şi coloane; să determine poziţia unui punct din primul cadran dacă se ştiu coordonatele şi reciproc.
|
Problema |
|
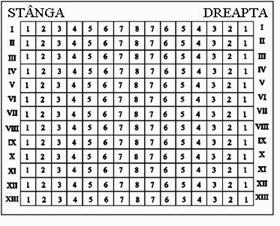
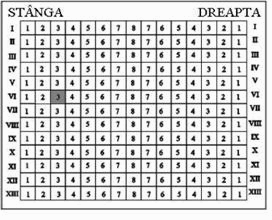
În imagine este redat planul
cinematografului "Odeon". Mircea ş-a cumpărat un bilet în rândul al
şaselea, locul 3, din stânga.
|
|
Soluţia |
|
|
МА.1.5.2. Elevul trebuie să ştie să citească datele de pe reprezentarea grafică, de pe diagramă sau din tabel şi să determine valoareaa minimă sau maximă a unei mărimi.
|
Problema |
|
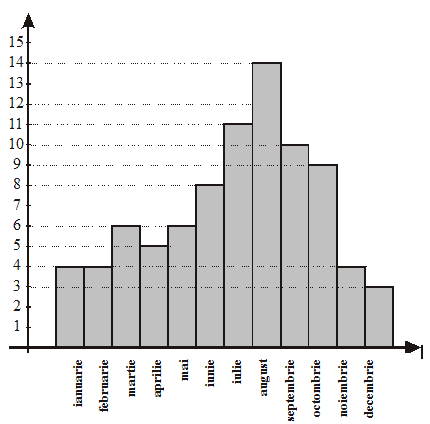
Numărul de zile cu soare dintr-un an este reprezentat în diagramă. a) Cele mai puţine zile cu soare au fost în luna ___________. b) Cele mai multe zile cu soare au fost în luna ___________. |
|
Soluţia |
|
a) Cele mai puţine zile cu soare au fost în luna decembrie. b) Cele mai multe zile cu soare au fost în luna august. |
МА.1.5.3. Elevul treuie să ştie să reprezinte datele, din tabel, pe grafic şi invers.
|
Problema |
||||||||||||
|
Cu ajutorul tabelului care reprezintă succesul la o teză,
completează repezentarea grafică, aşa cum este indicat.
|
||||||||||||
|
Soluţia |
||||||||||||
|
|
||||||||||||
МА.1.5.4. Elevul ştie să determine procentul dat dintr-o anumită mărime.
|
Problema |
|
Marcela a hotărât să-şi cumpere abţibilduri cu preţul de 4 000 de dinari. La magazin, vânzătorul i-a acordat o reducere de 10%. Cât este reducerea exprimată în dinari?
Marcela a avut o reducere de ______ dinari. |
|
Soluţia |
|
Marcela a avut o reducere de 400 de dinari. |
МА.2.1.1. Elevul trebue să ştie să compare, după mărime, numerele scrise în forme diferite.
|
Problema |
||||
|
Fie numerele
Care este cel mai mic dintre numerele date? Dar cel mai mare? Cel mai mic număr este ________, iar cel mai mare număr este _______.
|
||||
|
Soluţia |
||||
|
Cel mai mic număr este -1,2, iar cel mai mare număr este 1 1/2. |
МА.2.1.2. Elevul trebue să ştie să determine numărul opus, valoarea reciprocă şi valoarea absolută a numărului dat, să calculeze valoarea unei expresii mai simple cu numere scrise în aceeaşi formă şi care conţine mai multe operaţii de rang diferit, inclusiv eliberarea de paranteze.
|
Problema |
|
Calculează:
|
|
Soluţia |
|
|
|
Problema |
|||||||||||||||
|
Completează tabelul ce urmează.
|
|||||||||||||||
|
Soluţia |
|||||||||||||||
|
|
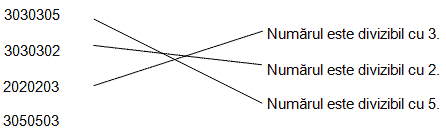
МА.2.1.3. Elevul trebue să ştie să aplice regulile de divizibilitate cu 2, 3, 5, 9 şi cu unităţile zecimale.
|
Problema |
|||||||||||||||||||||
|
Leagă numerele cu propoziţiile corespunzătoare.
|
|||||||||||||||||||||
|
Soluţia |
|||||||||||||||||||||
|
|
МА.2.1.4. Elevul trebue să ştie să aplice numerele şi expresiile numerice în situaţii reale mai simple.
|
Problema |
|
Pentru 25 de caiete s-au plătit 750 de
dinari. Un caiet este cu 20 de dinari mai scump decât un creion. Câte
creioane se puteau cumpăra cu aceeaşi sumă de bani?
Cu 750 de dinari se puteau cumpăra ________ creioane. |
|
Soluţia |
|
750 ׃ 25 = 30 Cu 750 de dinari se puteau cumpăra 75 de creioane. |
МА.2.2.1. Elevul a atins un nivel solid în aplicarea procedeelor de calcul şi poate să rezolve ecuaţii liniare şi sisteme de ecuaţii liniare cu două necunoscute.
|
Problema |
|
Înconjoară litera din faţa răspunsului corect. Soluţia ecuaţiei а) -20 şi-10; b) -10 şi 10; c) 10 şi 20; d) 20 şi 30. |
|
Soluţia |
|
c) 10 şi 20. |
МА.2.2.2. Elevul a atins un nivel solid în aplicarea procedeelor de calcul şi poate să opereze cu puteri şi să ştie ce este radicalul de ordinul doi.
|
Problema |
||||||||||||
|
Înconjoară cuvântul ADEVĂRAT, dacă afirmaţia este corectă sau FALS, dacă afirmaţia este incorectă.
|
||||||||||||
|
Soluţia |
||||||||||||
|
|
МА.2.2.3. Elevul a atins un nivel solid în aplicarea procedeelor de calcul şi poate să adune şi să scadă polinoame, să ştie să înmulţească două binoame şi să determine pătratul unui binom.
|
Problema |
|
Pătratul binomului ( а) b) c) d)
|
|
Soluţia |
|
b)
|
МА.2.2.4. Elevul a atins un nivel solid în aplicarea procedeelor de calcul şi poate să remarce dependenţa variabilelor, să ştie funcţia y=ax şi să interpreteze grafic proprietăţile ei, să facă legătura între aceste proprietăţi şi noţiunea de proporţionalitate directă şi să determine membrul necunoscut al proporţiei.
|
Problema |
|||||
|
Pe unul dintre desene este reprezentată grafic dependenţa dintre cantitatea de plumb (х) şi cantitatea de zinc (у) dintr-un aliaj, în care plumbul şi zincul sunt în raportul de 2:1. Înconjoară litera care este deasupra de graficul care reprezintă corect dependenţa dintre plumbul şi zincul din aliaj.
|
|||||
|
Soluţia |
|||||
|
c)
|
|
Problema |
|
8 m de pânză costă 2 400 de dinari. а) 12 m de pânză costă _______ de dinari. |
|
Soluţia |
|
а) 12 m de pânză costă 3600 de dinari. |
МА.2.2.5. Elevul a atins un nivel solid în aplicarea procedeelor de calcul şi poate să remarce dependenţa variabilelor şi să aplice ecuaţiile în rezolvarea problemelor textuale mai simple.
|
Problema |
|
După ce şi-a plătit creditul pentru telefonul mobil, cu o treime din economiile pe care le-a făcut, lui Petru i- au mai rămas 800 de dinari. Cât au fost economiile pe care le-a făcut Petru? Economiile lui Petru au fost de _______ dinari. |
|
Soluţia |
|
Economiile lui Petru au fost de 1200 dinari. |
МА.2.3.1. Elevul trebuie să ştie să determine unghiurile suplimentare şi complementare, unghiurile cu laturi paralele şi unghiurile opuse la vârf; să efectueze calculele dacă unghiurile sunt exprimate în grade întregi.
|
Problema |
||
|
||
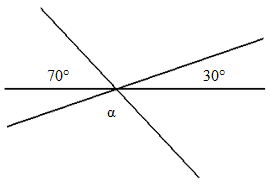
|
Soluţia |
||
|
α = 80° |
МА.2.3.2. Elevul trebuie să ştie să determine relaţiile între unghiurile şi laturile unui triunghi, suma unghiurilor unui triunghi şi ale unui patrulater şi să rezolve probleme aplicând teorema lui Pitagora.
|
Problema |
||||
|
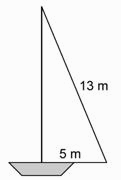
Care este aria velei din imagine? Scrie modul de rezolvare.
|
||||
|
Soluţia |
||||
|
Dacă catargul are înălţimea x, atunci x2 = 132 - 52 = 169 - 25 = 144.
Aria velei este 30 m2.
|
МА.2.3.3. Elevul trebuie să ştie să folosească formulele pentru a calcula lungimea circumferinţei, aria cercului şi a inelului circular.
|
Problema |
||
|
Cercul mai mic are aria de 9p cm2. Inelul circular are aria de 16p cm2. Calculează raza cercului mare.
|
||
|
Soluţia |
||
|
AcM = (9p + 16p) cm2 = 25p cm2 r2p= 25p cm2 r = 5 cm Raza cercului mare are 5 cm. |
МА.2.3.5. Elevul trebuie să ştie să calculeze aria şi volumul cilindrului, conului şi sferei, dacă elementele necesare sunt date direct în problemă.
|
Problema |
|
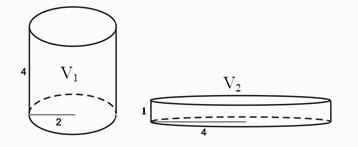
În imagine sunt două cilindre care au volumele V1 şi V2. Înconjoară litera din faţa răspunsului corect. а) V1 > V2 b) V1 < V2 c) V1 = V2 |
|
Soluţia |
|
c) V1 = V2 |
МА.2.3.6. Elevul trebuie să ştie să remarce figurile axial-simetrice şi să determine axa de simetrie; să folosească congruenţa şi să o asocieze cu proprietăţile caracteristice ale figurilor (de exemplu: paralelismul şi egalitatea laturilor paralelogramului).
|
Problema |
|
Umbreşte patru pătrate din imagine, astfel încât să obţii o figură simetrică în raport cu dreapta p.
|
|
Soluţia |
|
|
МА.2.4.1. Elevul trebuie să ştie să compare mărimile care sunt exprimate prin unităţi de măsură diferite pentru lungime şi masă.
|
Problema |
||||||||||||||
|
Profesoara a scris, pe tablă, masele a patru
obiecte.
|
||||||||||||||
|
Soluţia |
||||||||||||||
|
|
Problema |
|
Vânzătorul are trei pui în magazin. Masele lor sunt 1340 g, 1,35 kg şi respectiv 1kg 290 g. Scrie masele celor trei pui, în ordine, de la cea mai mică, la cea mai mare. Răspuns: ________ > _________ > ________ |
|
Soluţia |
|
1,35 kg > 1340 g > 1kg 290 g |
МА.2.4.2. Elevul trebuie să ştie să transforme o valută, în alta, aplicând corect proporţia necesară.
|
Problema |
|
Maria şi-a petrecut sărbătorile de iarnă în
Italia. Cheltuielile de călătorie au fost 200 de euro.
Maria a plătit_____________ dinari. |
|
Soluţia |
|
Maria a plătit 21000 de dinari. |
|
Problema |
|
O coroană norvegiană are valoarea de 12,50
dinari, iar un euro are valoarea de 105 dinari. Ce valoare au 10 euro,
exprimată în coroane norvegiene.
10 euro au valoarea de______coroane norvegiene. |
|
Soluţia |
|
10 euro au valoarea de 105 · 10 = 1050 dinari, 1050 : 12,5 = 84. 10 euro au valoarea de 84 de coroane norvegiene.
|
МА.2.4.3. Elevul trebuie să ştie să exprime mărimea dată prin valoarea aproximată.
|
Problema |
||||||||
|
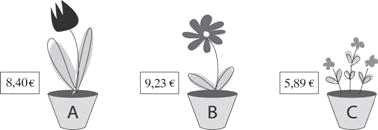
La florărie trebuie să aproximeze preţurile pentru florile din import, la cel mai apropiat număr întreg. Scrie preţurile noi.
|
||||||||
|
Soluţia |
||||||||
|
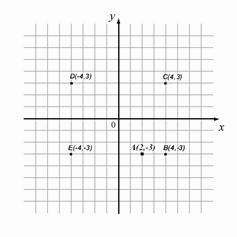
МА.2.5.1. Elevul trebuie să stăpânescă descrierea sistemului de coordonate (să determine coordonatele unui punct, ale punctului axial-simetric sau central-simetric etc).
|
Problema |
|
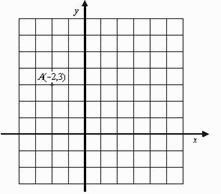
Desenează axa y, în baza coordonatelor punctului А care sunt date în sistemul cartezian de coordonate.
|
|
Soluţia |
|
|
МА.2.5.2. Elevul trebuie să ştie să citească diagrame şi tabele, iar în baza lor să prelucreze datele, respectând un criteriu (de exemplu: să determine media aritmetică pentru o mulţime de date; să compare valorile unui eşantion cu valoarea medie).
|
Problema |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
În tabel sunt date distanţele dintre oraşe exprimate în kilometri.
În baza datelor din tabel, completează afirmaţiile care urmează, astfel încât ele să fie adevărate. a) Distanţa de la Čačak, la Nikšić
este ______kilometri. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Soluţia |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a) Distanţa de la Čačak, la Nikšić
este 395 kilometri. |
МА.2.5.3. Elevul trebuie să prelucreze datele acumulate şi să le reprezinte tabelar sau grafic; să reprezinte valoarea medie prin mediană.
|
Problema |
||||||||||||||
|
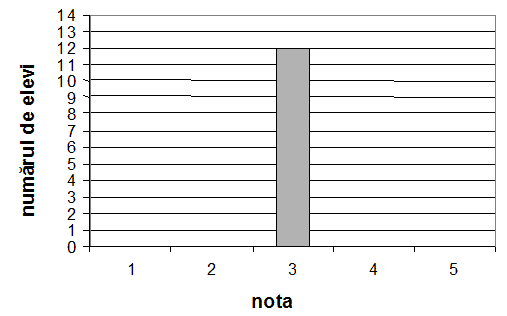
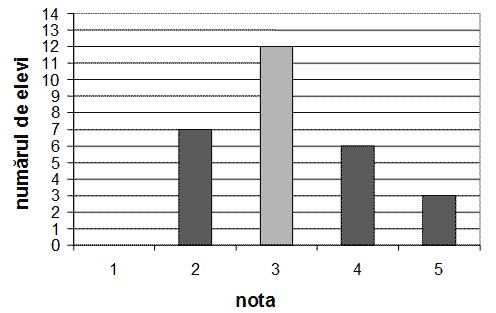
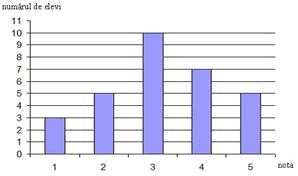
În imagine, diagrama reprezintă succesul unei clase obţinut la testul de matematică.
a) Completează tabelul care corespunde diagramei, aşa cum este indicat.
b) Calculează nota medie la testul de matematică. Nota medie la testul de matematică este________. |
||||||||||||||
|
Soluţia |
||||||||||||||
|
а)
b) Nota medie la testul de matematică este 3,2. |
||||||||||||||
МА.3.1.2. Elevul trebuie să ştie să opereze cu noţiunea de divizibilitate în situaţii problemă.
|
Problema |
|
Scrie trei numere din mia a cincea care au cifra zecilor 2 şi sunt divizibile cu 9.
Acestea sunt numerele: _____, _____, _____. |
|
Soluţia |
|
Trebuie scrise trei dintre numerele: {4023, 4122, 4221, 4320, 4329, 4428, 4527, 4626, 4725, 4824, 4923}. |
МА.3.1.3. Elevul trebuie să ştie să aplice numerele şi expresiile numerice în situaţii reale.
|
Problema |
|
O florăreasă face şi vinde buchete de flori. În fiecare buchet sunt 4 trandafiri şi 3 margarete. Să presupunem că florăreasa ar câştiga câte 35 de dinari la fiecare trandafir şi câte 25 de dinari la fiecare margaretă. Care este cel mai mic număr de buchete pe care trebuie să le vândă florăreasa, pentru a câştiga mai mult de 1500 de dinari? Scrie modul de rezolvare.
Florăreasa trebuie să vândă cel puţin _____ buchete. |
|
Soluţia |
|
Câştigul la un buchet este: 4 • 35 + 3 • 25 + 60 = 140 + 75 + 60 = 275 275 • 5 = 1375, 275 • 6 = 1650 sau 1500 : 275 = 5,45… Florăreasa trebuie să le vândă cel puţin 6 buchete. |
МА.3.2.2. Elevul a atins un nivel superior în efectuarea de operaţii, prin sublinierea proprietăţilor care se aplică şi ştie să folosească proprietăţile puterilor şi ale radicalilor de ordinul doi.
|
Problema |
|
Se ştie că 322 = 1024. Calculează: а) b) c) |
|
Soliţia |
|
а) b) c)
|
МА.3.2.3. Elevul a atins un nivel superior în efectuarea de operaţii, prin sublinierea proprietăţilor care se aplică şi ştie să aplice formulele pentru diferenţa de pătrate şi pentru pătratul binomului, să transforme eficient expresiile algebrice şi să le aducă la forma cea mai simplă.
|
Problema |
|
Înconjoară ltera din faţa răspunsului corect. Polinomul (а - 1)(2а + 1) - (а - 6)(а + 6) este egal cu polinomul: a) а2 − а + 35 b) а2 − а − 37 c) а2 + 35 d) а2 − 37 |
|
Soluţia |
|
а) а2 − а + 35 |
|
Problema |
|
Calculează: а) diferenţa pătratelor 7 şi 3; _____________________________________ b) pătratul diferenţei numerelor 7 şi 3; _______________________________ c) suma pătratelor numerelor 7 şi 3;_________________________________ d) pătratul sumei numerelor 7 şi 3; __________________________________ |
|
Soluţia |
|
а) 72 - 32 = 49 - 9 = 40 b) (7 − 3)2 = 42 = 16 c) 72 + 32 = 49 + 9 = 58 d) (7 + 3)2 = 102 = 100 |
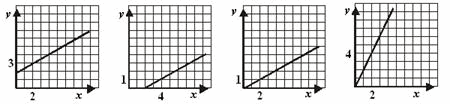
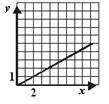
МА.3.2.4. Elevul a atins un nivel superior în efectuarea de operaţii, prin sublinierea proprietăţilor care se aplică şi ştie să facă diferenţa dintre mărimile direct proporţionale şi cele invers proporţionale şi să le exprime în forma corespunzătoare. Ştie funcţia liniară şi ştie să exprime grafic proprietăţile ei.
|
Problema |
||||||||
|
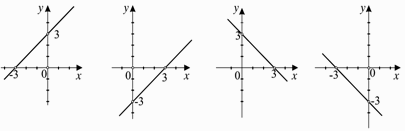
Care dintre graficele care urmează este
graficul funcţiei y = −x + 3?
|
||||||||
|
Soluţia |
||||||||
|
|
||||||||
|
Problema |
|
Nouă prieteni ar fi curăţat un bazin în patru zile. Câţi prieteni ar trebui să-i ajute pentru ca bazinul să fie curăţat în trei zile? Bazinul va fi curăţat în trei zile dacă îi ajută încă ____ prieteni. |
|
Soluţia |
|
9 : x = 3 : 4 sau x : 9 = 4 :
3. Bazinul va fi curăţat în trei zile dacă îi ajută încă 3 prieteni. |
МА.3.2.5. Elevul a atins un nivel superior în efectuarea de operaţii, prin sublinierea proprietăţilor care se aplică şi ştie să aplice ecuaţiile, inecuaţiile şi sistemele da ecuaţii liniare în rezolvarea problemelor textuale mai complexe.
|
Problema |
|
Cât timp a fost în vacanţă, Cornelia le-a
trimis celor 9 prietene, din bloc, câte o scrisoare sau ilustrată. Timbrele
pentru ilustrate sunt de câte 10 dinari, iar cele pentru scrisori sunt de
câte 15 dinari. Câte ilusteate şi câte scrisori a expediat Cornelia dacă,
pentru timbre, a plătit în total 110 dinari.
Cornelia a expediat_________scrisori şi________ilustrate. |
|
Soluţia |
|
x -
numărul de scrisori x + y
= 9 Soluţia sistemului este x = 5 şi y = 4, oricare ar fi metoda de rezolvare. Cornelia a expediat 5 scrisori şi 4 ilustrate. |
МА.3.3.1. Elevul trebuie să ştie să efectueze calcule cu unghiuri, inclusiv cazul în care măsura unghiului trebuie transformată; să conchidă, aplicând proprietăţile dreptelor paralele şi perpendiculare, inclusiv proprietăţile unghiurilor formate de o secantă.
|
Probleme |
||
|
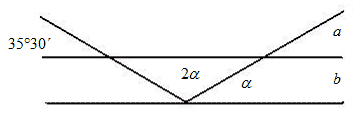
Determină cât este unghiul a, dacă sunt paralele dreptele a şi b.
|
||
|
Soluţia |
||
|
Unghiul a =48°10΄ |
МА.3.3.2. Elevul trebuie să ştie să aplice proprietăţile de bază ale triunghiului, patrulaterului, paralelogramului şi ale trapezului; să calculeze perimetrele şi ariile acestora cu ajutorul elementelor care nu sunt date, neapărat, direct în textul problemelor; să ştie să construiască figurile amintite mai sus.
|
Problema |
||
|
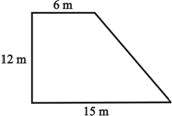
Câţi metri de sârmă sunt necesari pentru a împrejmui o curte care are forma de trapez dreptunghic ca cel din imagine? Scrie modul de rezolvare.
Sunt necesari_____metri de sârmă.
|
||
|
Soluţia |
||
Sunt necesari 48 metri de sârmă. |
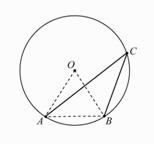
МА.3.3.3. Elevul trebuie să ştie să determine unghiul la centru şi unghiul înscris în cerc, să calculeze aria sectorului de cerc şi lungimea arcului de cerc.
|
Problema |
|
Calculează unghiul ACB dacă raza cercului este egală cu coarda AB.
Ð ACB = ______
|
|
Soluţia |
|
Ð ACB = 30° |
|
Problema |
|
De câte ori este mai mică aria sectorului de cerc decât aria cercului, dacă unhiul la centru are 30°?
Este mai mică de____ori. |
|
Soluţia |
|
Este mai mică de 12 ori. |
МА.3.3.4. Elevul trebuie să ştie să calculeze ariile şi volumele prismelor şi piramidelor, inclusiv cazurile când elementele necesare nu sunt date direct în problemă.
|
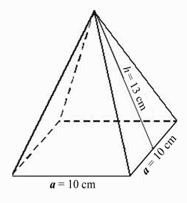
Problema |
||
|
Calculează volumul piramidei patrulatere regulate dacă se ştie că muchia bazei este a = 10 cm, iar înălţimea feţei laterale este h = 13 cm. Scrie modul de rezolvare.
|
||
|
Soluţia |
||
|
Volumul piramidei este de 400 cm3.
|
МА.3.3.5. Elevul trebuie să ştie să calculeze aria şi volumul cilindrului, conului şi sferei, inclusiv cazurile în care elementele necesare nu sunt date direct în problemă.
|
Problema |
|
Înconjoară ltera din faţa răspunsului corect. Triunghiul dreptunhic, ale cărui catete sunt а = 9 cm şi b = 12 cm, se roteşte în jurul catetei b. Raportul dintre aria bazei şi aria laterală a conului obţinut prin rotaţie este: а) 1 : 1; b) 3 : 4; c) 3 : 5; d) 4 : 5. |
|
Soluţia |
|
c) 3 : 5 |
|
Problema |
|
Care este aria mingii celei mai mari pe care o putem împacheta într-o cutie care are forma de cub cu muchia de 20 cm?
Aria mingei este____cm. |
|
Soluţia |
|
Aria mingei este 36p cm. |
МА.3.3.6. Elevul trebuie să ştie să aplice congruenţa şi asemănarea triunghiurilor, legând, în felul acesta, proprietăţile diferite ale obiectelor geometrice.
|
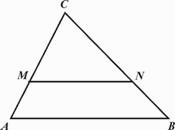
Problema |
||
|
Segmentul MN este paralel cu segmentul АВ. Cât este raportul СМ : MА, dacă se ştie că MN : AB = 2 : 3? Înconjoară ltera din faţa răspunsului corect.
|
||
|
Soluţia |
||
|
а) 2 : 1 |
|
Problema |
||||||||||||
|
Înconjoară cuvântul Adevărat, dacă afirmaţia este adevărată, iar dacă este falsă, atunci înconjoară cuvântul Fals.
|
||||||||||||
|
Soluţia |
||||||||||||
|
MА.3.4.2. Elevul trebuie să ştie să estimeze, să aproximeze datele şi să efectueze calcule cu valori aproximate; să exprime aprecierea erorii (de axemplu: mai puţin de 1 dinar, 1 cm, 1 g etc).
|
Problema |
|
Distanţa de la localitatea A, la localitatea D este reprezentată pe desenul ce urmează.
Gloria a estimat distanţa dintre localităţile А şi D, prin aproximarea fiecărei dintre distanţe, la cel mai apropiat număr de kilometri întregi şi le-a adunat. Cornelia a adunat distanţele de pe desen, iar rezultatul l-a aproximat la numărul cel mai apropiat de kilometri întregi. Înconjoară ltera din faţa răspunsului corect. а) Gloria a obţinut un număr mai mare decât Cornelia. b) Gloria şi Cornelia au obţinut numere egale. c) Gloria a obţinut un număr mai mic decât Cornelia. |
|
Soluţia |
|
а) Gloria a obţinut un număr mai mare decât Cornelia. |
МА.3.5.1. Elevul trebuie să ştie să determine poziţia (coordonatele) punctelor care satisfac condiţii mai complexe.
|
Problema |
|
Desenează, pe sistemul de coordonate, toate punctele care sunt la aceeaşi distanţă, faţă de axa x, ca şi punctul А şi a căror distanţă faţă de axa y este de două ori mai mare decât distanţa punctului A faţă de axa y.
|
|
Soluţia |
|
|
МА.3.5.2. Elevul trebuie să ştie să interpreteze diagrame şi tabele.
|
Problema |
||||||||||||||||||||||||||||||||||||||||||||||||
|
În tabel sunt date distanţele, dintre unele oraşe, exprimate în kilometri.
а) Care oraş este la distanţa de 115 km faţă de Belgrad?....................... b) Distanţa dintre care oraşe este 353 km?............................................... c) Distanţa dintre care oraşe este mai mică de 50 km?.......................................... d) Câte oraşe din tabel sun la mai mult de 200 km faţă de Belgrad?.........
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Soluţia |
||||||||||||||||||||||||||||||||||||||||||||||||
|
а) Kragujevac; b) Kraljevo şi Subotica; c) Jagodina şi Kragujevac; d) Trei. |
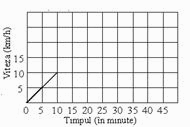
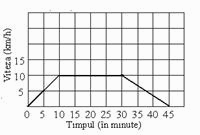
МА.3.5.3. Elevul trebuie să ştie să acumuleze şi să prelucreze datele şi să alcătuiască singur/singură diagrame sau tabele; să ştie să deseneze graficul prin care se exprimă dependenţa mărimilor.
|
Problema |
|
Maria a mers cu bicicleta 45 de minute. După 10 minute de mers a ajuns la viteza de 10 km/h. A mers cu această viteză următuarele 20 de minute, iar apoi a încetinit uniform până la oprire. Completează digrama ce reprezintă mişcarea Mariei, aşa cum este indicat. |
|
Soluţia |
|
|
МА.3.5.4. Elevul trebuie să ştie să aplice calculul procentual în situaţii complexe.
|
Problema |
|
Preţul unei cărţi este mărită cu 10%, mai întâi, iar apoi este micşorat cu 10% şi acum este 198 de dinari. Cât a fost preţul cărţii înainte de scumpire? Înconjoară ltera din faţa răspunsului corect. а) 198 de dinari; b) 200 de dinari; c) 202 dinari; d) 196,02 dinari. |
|
Soluţia |
|
b) 200 de dinari. |
Normele pentru nivelul de cunoştinţe care se plică la sfârşitul ciclului de învăţământ obligatoriu pntru matematică se vor aplica prin probleme neunoscute.
МА.2.3.4. Elevul trebuie să ştie să dispună de noţiunile de prizmă şi piramidă; să calculeze ariile şi volumele acestora, dacă elementele necesare sunt date direct în problemă.
|
Problema |
|
Muchia bazei unei piramide triunghiulare echilatere are 8 cm. Care este aria acesei piramide? Scrie modul de rezolvare.
Aria piramidei are ___________ cm2 |
|
Soluţia |
|
sau
Aria piramidei ete de 64
|
МА.2.5.4. Elevul trebuie să aplice calculul procentual în situaţii reale simple (de exemplu: schimbarea preţului unui produs cu un procent dat).
|
Problema |
|
Gloria vinde îngheţată. Preţul unei îngheţate este 60 de dinari. Câştigul Gloriei este de 6 dinari la fiecare îngheţată. Care este câştigul la fiecare îngheţată exprimat în procente? Înconjoară răspunsul din faţa răspunsului corect. а) 6 % b) 1 % c) 54 % d) 10 % |
|
Soluţie |
|
d) 10 % |
МА.3.1.1. Elevul trebuie să ştie să determine valoarea numerică a unei expresii numerice mai complexe.
|
Problema |
|
Calculează podusul expresiilor A şi B, dacă А = _______, B = ______, produsul A · B = _______
|
|
Soluţia |
|
А = 3, B = 2/3, produsul A · B = 2.
|
МА.3.2.1. Elevul a atins un nivel superior în efectuarea operaţiilor, prin sublinierea proprietăţilor care se aplică şi ştie să compună şi să rezolve ecuaţii, inecuaţii şi sisteme de ecuaţii liniare cu două necunoscute.
|
Problema |
|
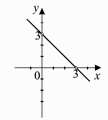
Care este mulţimea de numere, de pe dreapta
numerică, care sunt soluţiile inecuaţiei: Înconjoară ltera din faţa răspunsului corect.
|
|
Soluţia |
|
|
МА.3.4.1. Elevul trebuie să ştie să transforme unităţile de măsură, atunci când efectuează calcule cu ele.
|
Problema |
|
Un film s-a teriminat la ora 22 şi 10 minute. Când a început filmul dacă se ştie că el a durat 115 minute? Înconjoară ltera din faţa răspunsului corect. а) la ora 20 şi 55 de minute; b) la ora 20 şi 45 de minute; c) la ora 20 şi 15 minute; d) la ora 20 şi 5 minute. |
|
Soluţia |
|
c) la ora 20 şi 15 minute. |